Figure 2a:
Stochastic simulation run including all encapsidation (chain)
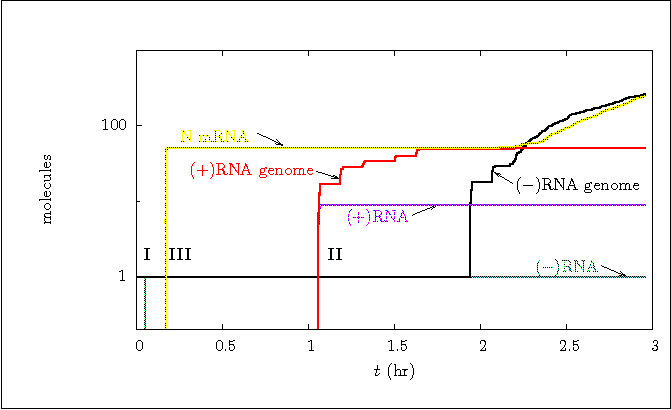
Code for Figure 2a
Text of the GNU GPL.
main.m
clear all
format compact
% set seeds for reproducible runs
rand ("seed", -1)
randn("seed", -1)
% Initiation
tol=0.01; % maximum allowed change (0.01 = 1%) in Langevin species per time step;
max_step=10; % maximum allowed time step, when no stochastic reaction occurs;
checksize = 100; % species level has to be higher than checksize to switch to Langevin implementation
runs=1; % number of simulation runs
% Kinetic paramters:
factor=1.29e9; % conversion factor for the parameters found in the literature
% (L/mol/sec --> n/sec): factor = 4/3 * pi * (16e-6/2)^3 * 6.022e23; volume*Avogadro
% (The average cell is assumed to be spheric with a radius of 16 micrometers)
k2=0.0755; % protein translation rate per mRNA
k3=(4e7+7.9e7)/2/factor; % transcription and replication initiation, average of 2 Qbeta (Werner 1991)
k1=[1 .75 .5625 .422 .422 .0633]*k3; % transcritption and replication initiation rate
% Initial condition:
y=[1 zeros(1,2523) 1258 466 1826 1205 0 50 2.962e11]; % initial condition of all states
% max_events sets the maximum number of stored events for delayed reactions
% the smaller these arrays are, the faster you can look up the time stamps of the stored delayed reactions
max_events1 = 5000;
max_events2 = 4500;
max_events3 = 4000;
max_events4 = 3500;
max_events5 = 3000;
max_events6 = 600;
max_events7 = 8000;
max_events8 = 2000;
max_events9 = 3000;
max_events10 = 3000;
max_events11 = 3000;
max_events12 = 3000;
max_events13 = 4000;
max_events14 = 700;
max_events15 = 9000;
max_events16 = 4000;
max_events17 = 1000;
% Delays
nuc_length=[1333;822;838;1672;720;6380]; % nucleotide length
tau=((cumsum(nuc_length)./3.7))+cumsum(240*ones(6,1)); % delays for transcription (time to transcribe the gene + stop time (240 secs) at each gene junction (4 mins))
tau(7:8)=sum(nuc_length)/3.7; % delays for replication (time to replicate the genome, NO stop time at gene junctions)
% Start of simulation:
for u=1:runs % Loop for all simulation runs
% First part of simulation
% No fast switching N species, therefore, all states are modeled and only 15000 iterations or about 2.5 hours, whatever comes first
maxi=100000; % maximum number of iterations in the first part of the simulation
tend=14400; % maximum simulated time
% v1: stoichiometric matrix of the non-delayed reactions
% v2: stoichiometric matrix of the delayed reactions
v1=zeros(2531,2531);
v2=zeros(15,2531);
v1(1,2530)=-1;
v1(2:1259,2525)=-1;
for j=2:1259
v1(j,j-1)=-1;v1(j,j)=1;
end
v1(1260,2530)=-1;
v1(1261:2518,2525)=-1;
for j=1261:2518
v1(j,j-1)=-1;v1(j,j)=1;
end
for j=2519:2524
v1(j,2530)=-1;
end
for j=2525:2530
v1(j,j)=1;
end
v1(2525,2531)=-444;
v1(2526,2531)=-274;
v1(2527,2531)=-279;
v1(2528,2531)=-557;
v1(2529,2531)=-240;
v1(2530,2531)=-2127;
for j=2519:2524
v2(j-2518,j)=1;
end
v2(7,1)=1;
v2(8,1260)=1;
v2(9:15,2530)=1;
% event times et of all delayed reactions are initially set to inf
et1 = Inf * ones (max_events1, 1);
et2 = Inf * ones (max_events2, 1);
et3 = Inf * ones (max_events3, 1);
et4 = Inf * ones (max_events4, 1);
et5 = Inf * ones (max_events5, 1);
et6 = Inf * ones (max_events6, 1);
et7 = Inf * ones (max_events7, 1);
et8 = Inf * ones (max_events8, 1);
et9 = Inf * ones (max_events9, 1);
et10 = Inf * ones (max_events10, 1);
et11 = Inf * ones (max_events11, 1);
et12 = Inf * ones (max_events12, 1);
et13 = Inf * ones (max_events13, 1);
et14 = Inf * ones (max_events14, 1);
et15 = Inf * ones (max_events15, 1);
et16 = Inf * ones (max_events16, 1);
et17 = Inf * ones (max_events17, 1);
% Initialization (has to be done for each simulation);
T = zeros(maxi,1); % time vector
x = zeros(maxi,2531); % state vector for all states
x_tau = zeros(7,2531); % states of the past, only needed for delayed reactions that will be implemented with Langevin equations (continuous part)
genomes = zeros(maxi,1); % all (-)RNA genomes that are not fully encapsidated (still produce mRNAs and not used for replication)
T(1) = 0; % initial time
x(1,:) = y; % initial state
current_time = 0; % current simulation time (needed for storage of delayed reactions)
a = zeros(2531,1); % all reaction rates
rd = zeros(2531,1); % all continuous reaction rates
r_con = zeros(2531,1); % all continuous reaction rates that do not take part in the stochastic time step / reaction calculation
sd = zeros(2531,1); % all Langevin reaction rates
s_con = zeros(2531,1); % all Langevin reaction rates that do not take part in the stochastic time step / reaction calculation
%checks for fast and slow reactions Default to slow.
flag = ones(2531,1); % flags for non-delayed reactions, 1 for stochastic, 0 for Langevin implementation
flagp= ones(2531,1); % flags for delayed reactions, 1 for stochastic, 0 for Langevin implementation
pos=ones(17,1); % index of all stored delayed reactions (some reactions have more than one product at different times)
% Start of first part of the simulation until quasi-steady state of N is reached
for i=1:maxi-1
genomes(i)=sum(x(i,1:1258)); % all (-)RNA genomes that are not fully encapsidated (still produce mRNAs and not used for replication)
% Calculation of all reaction rates:
a(1) = 50*k1(1)*x(i,2518)*x(i,2530);
a(2:1259) = k3*x(i,1:1258).*x(i,2525);
a(1260) = k1(1)*x(i,1259)*x(i,2530);
a(1261:2518) = k3*x(i,1260:2517).*x(i,2525);
a(2519:2524) = k1(1:6).*genomes(i).*x(i,2530);
a(2525:2530) = k2.*x(i,2519:2524);
% Flags 2525 to 2530: (translation)
for j=2525:2530
if x(i,j) there are continuous reactions
if flag_mult == 0 % if there are continuous reactions
% Calculate the maximum step size:
% Calculation of all continuous reaction rates
r_con=zeros(2531,1);
for j=2525:2531
rd(j)=a(j)*(1-flag(j));
end
r_con(2525)=rd(2525);
r_con(2526)=rd(2526);
r_con(2527)=rd(2527);
r_con(2528)=rd(2528);
r_con(2529)=rd(2529);
r_con(2530)=rd(2530);
r_con(2531)=-rd(2525)*444-rd(2526)*274-rd(2527)*279-rd(2528)*557-rd(2529)*240-rd(2530)*2127; % Amino acid depletion (host resource)
% All current states to calculate the relative rate of change ?????(earliest switch occurs at checksize (100))?????
rr = r_con(2525:2531); % contiunous reaction rates
r_index = find(rr); % which reactions are continuous
r_new = rr(r_index); % r_new reacion rates are all non-zero
% last molecule level of continuous states:
w = x(i,2525:2531)';
w_new=w(r_index);
% time to change 100% in one state:
t_norm=w_new./r_new;
% maximum step: minimum of max_step and tolerance percentage multiplied with the smallest time
maxstep=min([max_step;tol*min(abs(t_norm))]);
% maxstep=min(abs(x_norm));
end; %End of calculating the maximum step size.
check_step = 0;
% All stochastic reaction rates:
r=a.*flag;
% Sum of it:
a0 =sum(r);
if (a0 == 0) %If there are no stochastic reactions
step = maxstep;
check_step = 1;
else
%Find timestep:
step = (1/a0)*log(1/r1);
%Find reaction:
m=sum(cumsum(r)<=r2*a0)+1; %Calculating which reaction occurs
if step > maxstep
check_step = 1;
%If the step is too big, only let it go a little bit.
%This is fine because the timesteps are exponentially distributed (and therefore memoryless).
step = maxstep;
m=0;
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%END OF STOCHASTIC CALCULATION%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Save current time for check of delayed reactions:
current_time=T(i)+step;
event_times=[et1(1) et2(1) et3(1) et4(1) et5(1) et6(1) et7(1) et8(1) et9(1) et10(1) et11(1) et12(1) et13(1) et14(1) et15(1)]; % All first event times
et=min(event_times); % first event time of all first event times
n=find(event_times==et); % which event comes first
n=n(1);
if et>current_time % if stored events are later than the next reaction:
%New states:
if m==0 % If no stochastic reaction (time step too big for continuous update) do nothing
else % else
z=v1(m,:); % Take the m-th row of the stoichiometric matrix v
end
% If reactions are delayed, store the completion of the reaction in seperate event vectors and move the pointer of the next free
% storage postition (makes storing and accesing the next event faster)
% m==2519...2525: transcription reactions
% m==1 and m==1260: replication reactions
if m==2519
et1(pos(1))=current_time+tau(1);
et9(pos(9))=current_time+tau(1);
pos(1)=pos(1)+1;
pos(9)=pos(9)+1;
end;
if m==2520
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et10(pos(10))=current_time+tau(2);
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(10)=pos(10)+1;
end;
if m==2521
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et11(pos(11))=current_time+tau(3);
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(11)=pos(11)+1;
end;
if m==2522
et4(pos(4))=current_time+tau(4);
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et12(pos(12))=current_time+tau(4);
pos(4)=pos(4)+1;
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(12)=pos(12)+1;
end;
if m==2523
et5(pos(5))=current_time+tau(5);
et4(pos(4))=current_time+tau(4);
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et13(pos(13))=current_time+tau(5);
pos(5)=pos(5)+1;
pos(4)=pos(4)+1;
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(13)=pos(13)+1;
end;
if m==2524
et6(pos(6))=current_time+tau(6);
et5(pos(5))=current_time+tau(5);
et4(pos(4))=current_time+tau(4);
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et14(pos(14))=current_time+tau(6);
pos(6)=pos(6)+1;
pos(5)=pos(5)+1;
pos(4)=pos(4)+1;
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(14)=pos(14)+1;
end;
if m==1
et7(pos(7))=current_time+tau(7);
et15(pos(15))=current_time+tau(7);
pos(7)=pos(7)+1;
pos(15)=pos(15)+1;
end;
if m==1260
et8(pos(8))=current_time+tau(7);
et15(pos(15))=current_time+tau(7);
pos(8)=pos(8)+1;
pos(15)=pos(15)+1;
end;
else %if there are stored events that are earlier than the next reaction
step = et - T(i); % update to the next event time
z = v2(n,:); % add delayed reaction
% delete the first event of the event vector and move the pointer of the last event one spot to the left
switch n
case{1}
et1 = [et1(2:length(et1));inf];
pos(1)=pos(1)-1;
case{2}
et2 = [et2(2:length(et2));inf];
pos(2)=pos(2)-1;
case{3}
et3 = [et3(2:length(et3));inf];
pos(3)=pos(3)-1;
case{4}
et4 = [et4(2:length(et4));inf];
pos(4)=pos(4)-1;
case{5}
et5 = [et5(2:length(et5));inf];
pos(5)=pos(5)-1;
case{6}
et6 = [et6(2:length(et6));inf];
pos(6)=pos(6)-1;
case{7}
et7 = [et7(2:length(et7));inf];
pos(7)=pos(7)-1;
case{8}
et8 = [et8(2:length(et8));inf];
pos(8)=pos(8)-1;
case{9}
et9 = [et9(2:length(et9));inf];
pos(9)=pos(9)-1;
case{10}
et10 = [et10(2:length(et10));inf];
pos(10)=pos(10)-1;
case{11}
et11 = [et11(2:length(et11));inf];
pos(11)=pos(11)-1;
case{12}
et12 = [et12(2:length(et12));inf];
pos(12)=pos(12)-1;
case{13}
et13 = [et13(2:length(et13));inf];
pos(13)=pos(13)-1;
case{14}
et14 = [et14(2:length(et14));inf];
pos(14)=pos(14)-1;
case{15}
et15 = [et15(2:length(et15));inf];
pos(15)=pos(15)-1;
end;
end;
% Continuous Langevin reaction rate calculations
if flag_mult==0 % if there are continuous reactions
rn = randn([6,1]); % normally distributed random number
for j=2525:2530
sd(j)=rd(j)*step+sqrt(rd(j)*step)*rn(j-2524); % first order Langevin equation
end
% set Langevin reaction rates
s_con(2525)=sd(2525);
s_con(2526)=sd(2526);
s_con(2527)=sd(2527);
s_con(2528)=sd(2528);
s_con(2529)=sd(2529);
s_con(2530)=sd(2530);
s_con(2531)=-sd(2525)*444-sd(2526)*274-sd(2527)*279-sd(2528)*557-sd(2529)*240-sd(2530)*2127;
r_con=s_con;
else
r_con=zeros(2531,1);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%delta x (stochastic and Langevin part together)
z=z+r_con';
%update all states
x(i+1,:) = x(i,:) + z;
%update time
T(i+1) = T(i) + step;
% if (mod(i,2000)==0)
% fprintf(1,'i=%3d T=%3.2f ',i,T(i));
% end;
% jump to next implementation part when tend is reached or all amino
% acids are depleted (which actually never happens)
if T(i+1)>tend || x(i+1,2531)<=0
break
end
end
message = ['End of run ',num2str(u),' with ',num2str(i),' iterations']
end
%% store results at times given in tplot
%% use 1 second time interval for plotting
%tplot = linspace(T(1), T(end), 1)';
%% jbr, removing this linspace error introduced in changest 32
%% 12/25/2008
tplot = (T(1):1:T(end))';
[tcon, idx] = sort([T; tplot]);
test = (idx > length(T));
howmanyoldguys = cumsum(1-test);
trow = howmanyoldguys(test);
x1 = x(trow,1); % (-)RNA_0 genome
x2 = sum(x(trow,1:1259),2); % all (-)RNA genomes
x3 = x(trow,1259); % (-)RNA_{1258}
x4 = x(trow,1260); % (+)RNA genome
x5 = sum(x(trow,1260:2518),2); % all (+)RNA genomes
x6 = x(trow,2518); % (+)RNA_{1258}
x7 = x(trow,2519); % N mRNA
x8 = x(trow,2525); % N proteins
table = [tplot/3600, x1, x2, x3, x4, x5, x6 x7 x8] ;
save fullrun.dat table
