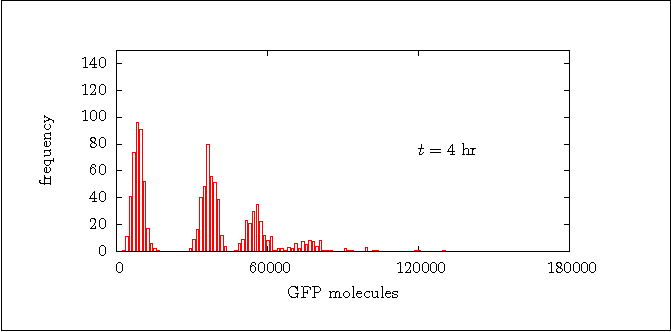
Figure 8b:
Distribution of the GFP at t = 4 hr.
Code for Figure 8b
Text of the GNU GPL.
main.m
clear all
format compact
% set seeds for reproducible runs
rand ("seed", -1)
randn("seed", -1)
% Initiation
tol=0.01; % maximum allowed change (0.01 = 1%) in Langevin species per time step;
max_step=10; % maximum allowed time step, when no stochastic reaction occurs;
checksize = 100; % species level has to be higher than checksize to switch to Langevin implementation
runs=1000; % number of simulation runs
%% runs=250; % smaller number of run for debugging
tfinal=14400; % simulation time 14400 secs = 4 hours
% Kinetic paramters:
factor=1.29e9; % conversion factor for the parameters found in the literature
% (L/mol/sec --> n/sec): factor = 4/3 * pi * (16e-6/2)^3 * 6.022e23; volume*Avogadro
% (The average cell is assumed to be spheric with a radius of 16 micrometers)
k2=0.0755; % protein translation rate per mRNA
k3=(4e7+7.9e7)/2/factor; % transcription and replication initiation, average of 2 Qbeta (Werner 1991)
k1=[1 .75 .5625 .422 .422 .0633]*k3; % transcritption and replication initiation rate
% Initial condition:
y=[1 zeros(1,2523) 1258 466 1826 1205 0 50 2.962e11]; % initial condition of all states
% max_events sets the maximum number of stored events for delayed reactions
% the smaller these arrays are, the faster you can look up the time stamps of the stored delayed reactions
max_events1 = 5000;
max_events2 = 4500;
max_events3 = 4000;
max_events4 = 3500;
max_events5 = 3000;
max_events6 = 600;
max_events7 = 8000;
max_events8 = 2000;
max_events9 = 3000;
max_events10 = 3000;
max_events11 = 3000;
max_events12 = 3000;
max_events13 = 4000;
max_events14 = 700;
max_events15 = 9000;
max_events16 = 4000;
max_events17 = 1000;
% Delays
nuc_length=[1333;822;838;1672;720;6380]; % nucleotide length
tau=((cumsum(nuc_length)./3.7))+cumsum(240*ones(6,1)); % delays for transcription (time to transcribe the gene + stop time (240 secs) at each gene junction (4 mins))
tau(7:8)=sum(nuc_length)/3.7; % delays for replication (time to replicate the genome, NO stop time at gene junctions)
% Calculations for Poisson distribution
p=zeros(101,1); % will later be assigned with the probability of being in states 0 to 100
facts = zeros(101,1); % factorials that will later be used to calculate the probability distribution
for j=1:101
facts(j) = gamma(j);
end
% Storing time and state vectors
% It would be impossible to store all runs and states
% We select a number of points in time and the states we want to store in order to reduce the amount of memory needed
time_vec=0:1:tfinal; % time vector, we store all states every second of the run
time_vec=time_vec';
for c=1:18
eval(['x',num2str(c),'=zeros(tfinal+1,runs);'])
end
% Start of simulation:
for u=1:runs % Loop for all simulation runs
% First part of simulation
% No fast switching N species, therefore, all states are modeled and only 15000 iterations or about 2.5 hours, whatever comes first
maxi=15000; % maximum number of iterations in the first part of the simulation
tend=10000; % maximum simulated time until switch into quasi-steady state implementation of the fast switching species
% v1: stoichiometric matrix of the non-delayed reactions
% v2: stoichiometric matrix of the delayed reactions
v1=zeros(2531,2531);
v2=zeros(15,2531);
v1(1,2530)=-1;
v1(2:1259,2525)=-1;
for j=2:1259
v1(j,j-1)=-1;v1(j,j)=1;
end
v1(1260,2530)=-1;
v1(1261:2518,2525)=-1;
for j=1261:2518
v1(j,j-1)=-1;v1(j,j)=1;
end
for j=2519:2524
v1(j,2530)=-1;
end
for j=2525:2530
v1(j,j)=1;
end
v1(2525,2531)=-444;
v1(2526,2531)=-274;
v1(2527,2531)=-279;
v1(2528,2531)=-557;
v1(2529,2531)=-240;
v1(2530,2531)=-2127;
for j=2519:2524
v2(j-2518,j)=1;
end
v2(7,1)=1;
v2(8,1260)=1;
v2(9:15,2530)=1;
% event times et of all delayed reactions are initially set to inf
et1 = Inf * ones (max_events1, 1);
et2 = Inf * ones (max_events2, 1);
et3 = Inf * ones (max_events3, 1);
et4 = Inf * ones (max_events4, 1);
et5 = Inf * ones (max_events5, 1);
et6 = Inf * ones (max_events6, 1);
et7 = Inf * ones (max_events7, 1);
et8 = Inf * ones (max_events8, 1);
et9 = Inf * ones (max_events9, 1);
et10 = Inf * ones (max_events10, 1);
et11 = Inf * ones (max_events11, 1);
et12 = Inf * ones (max_events12, 1);
et13 = Inf * ones (max_events13, 1);
et14 = Inf * ones (max_events14, 1);
et15 = Inf * ones (max_events15, 1);
et16 = Inf * ones (max_events16, 1);
et17 = Inf * ones (max_events17, 1);
% Initialization (has to be done for each simulation);
T = zeros(maxi,1); % time vector
x = zeros(maxi,2531); % state vector for all states
g = zeros(maxi,2); % g(:,1) = sum of all (-)RNA genomes but the naked strand, g(:,2) = sum of all (+)RNA genomes but the naked strand
x_tau = zeros(7,2531); % states of the past, only needed for delayed reactions that will be implemented with Langevin equations (continuous part)
genomes = zeros(maxi,1); % all (-)RNA genomes that are not fully encapsidated (still produce mRNAs and not used for replication)
alpha = zeros(maxi,1); % mean of fast switching species N (Poisson distribution)
T(1) = 0; % initial time
x(1,:) = y; % initial state
current_time = 0; % current simulation time (needed for storage of delayed reactions)
a = zeros(2531,1); % all reaction rates
rd = zeros(2531,1); % all continuous reaction rates
r_con = zeros(2531,1); % all continuous reaction rates that do not take part in the stochastic time step / reaction calculation
sd = zeros(2531,1); % all Langevin reaction rates
s_con = zeros(2531,1); % all Langevin reaction rates that do not take part in the stochastic time step / reaction calculation
%checks for fast and slow reactions Default to slow.
flag = ones(2531,1); % flags for non-delayed reactions, 1 for stochastic, 0 for Langevin implementation
flagp= ones(2531,1); % flags for delayed reactions, 1 for stochastic, 0 for Langevin implementation
pos=ones(17,1); % index of all stored delayed reactions (some reactions have more than one product at different times)
% Start of first part of the simulation until quasi-steady state of N is reached
for i=1:maxi-1
genomes(i)=sum(x(i,1:1258)); % all (-)RNA genomes that are not fully encapsidated (still produce mRNAs and not used for replication)
% Calculation of all reaction rates:
a(1) = 50*k1(1)*x(i,2518)*x(i,2530);
a(2:1259) = k3*x(i,1:1258).*x(i,2525);
a(1260) = k1(1)*x(i,1259)*x(i,2530);
a(1261:2518) = k3*x(i,1260:2517).*x(i,2525);
a(2519:2524) = k1(1:6).*genomes(i).*x(i,2530);
a(2525:2530) = k2.*x(i,2519:2524);
% Flags 2525 to 2530: (translation)
for j=2525:2530
if x(i,j) there are continuous reactions
if flag_mult == 0 % if there are continuous reactions
% Calculate the maximum step size:
% Calculation of all continuous reaction rates
r_con=zeros(2531,1);
for j=2525:2531
rd(j)=a(j)*(1-flag(j));
end
r_con(2525)=rd(2525);
r_con(2526)=rd(2526);
r_con(2527)=rd(2527);
r_con(2528)=rd(2528);
r_con(2529)=rd(2529);
r_con(2530)=rd(2530);
r_con(2531)=-rd(2525)*444-rd(2526)*274-rd(2527)*279-rd(2528)*557-rd(2529)*240-rd(2530)*2127; % Amino acid depletion (host resource)
% All current states to calculate the relative rate of change ?????(earliest switch occurs at checksize (100))?????
rr = r_con(2525:2531); % contiunous reaction rates
r_index = find(rr); % which reactions are continuous
r_new = rr(r_index); % r_new reacion rates are all non-zero
% last molecule level of continuous states:
w = x(i,2525:2531)';
w_new=w(r_index);
% time to change 100% in one state:
t_norm=w_new./r_new;
% maximum step: minimum of max_step and tolerance percentage multiplied with the smallest time
maxstep=min([max_step;tol*min(abs(t_norm))]);
% maxstep=min(abs(x_norm));
end; %End of calculating the maximum step size.
check_step = 0;
% All stochastic reaction rates:
r=a.*flag;
% Sum of it:
a0 =sum(r);
if (a0 == 0) %If there are no stochastic reactions
step = maxstep;
check_step = 1;
else
%Find timestep:
step = (1/a0)*log(1/r1);
%Find reaction:
m=sum(cumsum(r)<=r2*a0)+1; %Calculating which reaction occurs
if step > maxstep
check_step = 1;
%If the step is too big, only let it go a little bit.
%This is fine because the timesteps are exponentially distributed (and therefore memoryless).
step = maxstep;
m=0;
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%END OF STOCHASTIC CALCULATION%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Save current time for check of delayed reactions:
current_time=T(i)+step;
event_times=[et1(1) et2(1) et3(1) et4(1) et5(1) et6(1) et7(1) et8(1) et9(1) et10(1) et11(1) et12(1) et13(1) et14(1) et15(1)]; % All first event times
et=min(event_times); % first event time of all first event times
n=find(event_times==et); % which event comes first
n=n(1);
if et>current_time % if stored events are later than the next reaction:
%New states:
if m==0 % If no stochastic reaction (time step too big for continuous update) do nothing
else % else
z=v1(m,:); % Take the m-th row of the stoichiometric matrix v
end
% If reactions are delayed, store the completion of the reaction in seperate event vectors and move the pointer of the next free
% storage postition (makes storing and accesing the next event faster)
% m==2519...2525: transcription reactions
% m==1 and m==1260: replication reactions
if m==2519
et1(pos(1))=current_time+tau(1);
et9(pos(9))=current_time+tau(1);
pos(1)=pos(1)+1;
pos(9)=pos(9)+1;
end;
if m==2520
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et10(pos(10))=current_time+tau(2);
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(10)=pos(10)+1;
end;
if m==2521
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et11(pos(11))=current_time+tau(3);
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(11)=pos(11)+1;
end;
if m==2522
et4(pos(4))=current_time+tau(4);
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et12(pos(12))=current_time+tau(4);
pos(4)=pos(4)+1;
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(12)=pos(12)+1;
end;
if m==2523
et5(pos(5))=current_time+tau(5);
et4(pos(4))=current_time+tau(4);
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et13(pos(13))=current_time+tau(5);
pos(5)=pos(5)+1;
pos(4)=pos(4)+1;
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(13)=pos(13)+1;
end;
if m==2524
et6(pos(6))=current_time+tau(6);
et5(pos(5))=current_time+tau(5);
et4(pos(4))=current_time+tau(4);
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et14(pos(14))=current_time+tau(6);
pos(6)=pos(6)+1;
pos(5)=pos(5)+1;
pos(4)=pos(4)+1;
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(14)=pos(14)+1;
end;
if m==1
et7(pos(7))=current_time+tau(7);
et15(pos(15))=current_time+tau(7);
pos(7)=pos(7)+1;
pos(15)=pos(15)+1;
end;
if m==1260
et8(pos(8))=current_time+tau(7);
et15(pos(15))=current_time+tau(7);
pos(8)=pos(8)+1;
pos(15)=pos(15)+1;
end;
else %if there are stored events that are earlier than the next reaction
step = et - T(i); % update to the next event time
z = v2(n,:); % add delayed reaction
% delete the first event of the event vector and move the pointer of the last event one spot to the left
switch n
case{1}
et1 = [et1(2:length(et1));inf];
pos(1)=pos(1)-1;
case{2}
et2 = [et2(2:length(et2));inf];
pos(2)=pos(2)-1;
case{3}
et3 = [et3(2:length(et3));inf];
pos(3)=pos(3)-1;
case{4}
et4 = [et4(2:length(et4));inf];
pos(4)=pos(4)-1;
case{5}
et5 = [et5(2:length(et5));inf];
pos(5)=pos(5)-1;
case{6}
et6 = [et6(2:length(et6));inf];
pos(6)=pos(6)-1;
case{7}
et7 = [et7(2:length(et7));inf];
pos(7)=pos(7)-1;
case{8}
et8 = [et8(2:length(et8));inf];
pos(8)=pos(8)-1;
case{9}
et9 = [et9(2:length(et9));inf];
pos(9)=pos(9)-1;
case{10}
et10 = [et10(2:length(et10));inf];
pos(10)=pos(10)-1;
case{11}
et11 = [et11(2:length(et11));inf];
pos(11)=pos(11)-1;
case{12}
et12 = [et12(2:length(et12));inf];
pos(12)=pos(12)-1;
case{13}
et13 = [et13(2:length(et13));inf];
pos(13)=pos(13)-1;
case{14}
et14 = [et14(2:length(et14));inf];
pos(14)=pos(14)-1;
case{15}
et15 = [et15(2:length(et15));inf];
pos(15)=pos(15)-1;
end;
end;
% Continuous Langevin reaction rate calculations
if flag_mult==0 % if there are continuous reactions
rn = randn([6,1]); % normally distributed random number
for j=2525:2530
%% avoid some nuisance generation of complex values;
%% jbr, 12/21/2008
D = real(rd(j)*step);
D = max(0, D);
sd(j)=rd(j)*step+sqrt(D)*rn(j-2524); % first order Langevin equation
end
% set Langevin reaction rates
s_con(2525)=sd(2525);
s_con(2526)=sd(2526);
s_con(2527)=sd(2527);
s_con(2528)=sd(2528);
s_con(2529)=sd(2529);
s_con(2530)=sd(2530);
s_con(2531)=-sd(2525)*444-sd(2526)*274-sd(2527)*279-sd(2528)*557-sd(2529)*240-sd(2530)*2127;
r_con=s_con;
else
r_con=zeros(2531,1);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%delta x (stochastic and Langevin part together)
z=z+r_con';
%update all states
x(i+1,:) = x(i,:) + z;
% update all partially encapsidated genomes (for later calculations)
g(i+1,1)=sum(x(i,2:1258));
g(i+1,2)=sum(x(i,1261:2517));
%update time
T(i+1) = T(i) + step;
% if (mod(i,2000)==0)
% fprintf(1,'i=%3d T=%3.2f ',i,T(i));
% end;
% jump to next implementation part when tend is reached or all amino
% acids are depleted (which actually never happens)
if T(i+1)>tend || x(i+1,2531)<=0
break
end
end
%% Second loop
% Initialization:
start=i; % first iteration of the second part of the simulation
maxi2=120000; % maximum number of iterations in the second part of the simulation
tend=tfinal; % maximum simulated time, which is always smaller than t(start+120000)
if (sum(x(i,1260:2517))+sum(x(i,1:1258)))==0 % Only when there is no naked strand --> there might not me a quasi-steady state yet
warning_message=str('Possibly, steady-state not yet reached.')
alpha(i)=1;
tau_encap=inf;
else % Calculation of the mean alpha of the quasi-steady state distribution of N
alpha(i) = k2 * x(i,2519) / (k3*(sum(x(i,1260:2517))+sum(x(i,1:1258))));
tau_encap=1258/(k3*alpha(i)); % Average of the total encapsidation time (approximation): 1258 * r_encap
end
index1=find(x(i,2:1258)); % Find all partially encapsidated (-)RNA strands
for j=1:length(index1) % Set the remaining time for the full encapsidation of the partially encapsidated (-)RNA strands
et16(j)=T(i)+(1258-index1(length(index2)+1-j))/1258*tau_encap;
pos(16)=pos(16)+1; % Increase the pointer of the number of delayed (-)RNA encapsidations by 1
end
index2=find(x(i,1261:2517)); % Find all partially encapsidated (+)RNA strands
for j=1:length(index2) % Set the remaining time for the full encapsidation of the partially encapsidated (+)RNA strands
et17(j)=T(i)+(1258-index2(length(index2)+1-j))/1258*tau_encap;
pos(17)=pos(17)+1; % Increase the pointer of the number of delayed (+)RNA encapsidations by 1
end
tau_encap_old=tau_encap; % Set the old encapsidation time tau_encap_old to tau_encap (which will be used to update the end time of encapsidation)
% We reduce the number of states from more than 2500 to 19, because we do
% not model all intermediate states of the encapsidation (faster implementation)
x(:,1)=x(:,1); % (-)RNA (naked)
x(:,2)=g(:,1); % all partially encapsidated (-)RNA genomes
x(:,3)=x(:,1259); % fully encapsidated (-)RNA genome
x(:,4)=x(:,1260); % (+)RNA (naked)
x(:,5)=g(:,2); % all partially encapsidated (-)RNA genomes
x(:,6)=x(:,2518); % fully encapsidated (-)RNA genome
x(:,7:19)=x(:,2519:2531); % all other states: mRNAs and proteins and also the host resource amino acids in x(:,19)
x=[x(:,1:19);zeros(maxi2-i,19)]; % Reserve memory for all states and iterations
x_tau = zeros(7,19); % All past states at t-tau (tau = delay for all seven different delay times)
T=[T;zeros(maxi2-i,1)]; % Time vector
alpha=[alpha;zeros(maxi2-i,1)]; % Mean of N distribution vector
genomes=[genomes;zeros(maxi2-i,1)]; % genomes vector
a=zeros(19,1); % Calculation of all reaction rates:
ap=zeros(19,1); % Calculation of past reaction rates:
rd=zeros(19,1); % all continuous reaction rates
r_con=zeros(19,1); % all continuous reaction rates that do not take part in the stochastic time step / reaction calculation
sd = zeros(19,1); % all Langevin reaction rates
s_con=zeros(19,1); % all Langevin reaction rates that do not take part in the stochastic time step / reaction calculation
% v1: stoichiometric matrix of the non-delayed reactions
% v2: stoichiometric matrix of the delayed reactions
v1=zeros(19,19);
v2=zeros(17,19);
v1(1,18)=-1;
v1(2,1)=-1;v1(2,2)=1;
v1(4,18)=-1;
v1(5,4)=-1;v1(5,5)=1;
v1(7:12,18)=-1;
for j=13:18
v1(j,j)=1;
end
v1(13,19)=-444;
v1(14,19)=-274;
v1(15,19)=-279;
v1(16,19)=-557;
v1(17,19)=-240;
v1(18,19)=-2127;
for j=7:12
v2(j-6,j)=1;
end
v2(7,1)=1;v2(7,18)=1;
v2(8,4)=1;v2(8,18)=1;
v2(9:15,18)=1;
v2(16,2)=-1;v2(16,3)=1;
v2(17,5)=-1;v2(17,6)=1;
%checks for fast and slow reactions, Default to slow.
flag = ones(19,1); % flags for non-delayed reactions, 1 for stochastic, 0 for Langevin implementation
flagp= ones(19,1); % flags for delayed reactions, 1 for stochastic, 0 for Langevin implementation
%% Second Main Loop
for i=start:maxi2
genomes(i)=sum(x(i,1:2)); % all (-)RNA genomes that are not fully encapsidated (still produce mRNAs and not used for replication)
genomes2=(x(i,1)+x(i,2)+x(i,4)+x(i,5)); % all genomes that are involved in reactions with the N protein (only used for Poisson distribution of N)
% If there are no genomes that react with N, the genome level is set to N, such that we do not get an error message for dividing by 0
% It will not have an effect, as genomes2 is only used to calculate the mean of the distribution and the time delay, but not for the reaction
% rate, thus it will not have any effect on the stochastic reaction and time step
if genomes2==0
genomes2=1;
end
% Mean of the Poisson distribution of N
alpha(i) = k2 * x(i,7) / (k3*genomes2);
% Average time of encapsidation (1258 * delta_t) which is our way to simplify all encapsidation reactions to one reaction
tau_encap=1258/(k3*alpha(i));
% Update all encapsidation completion times with the newly calculated tau_encap
et16(1:pos(16))=T(i)+(et16(1:pos(16))-T(i))./tau_encap_old.*tau_encap; % encapsidation completion times for the (-)RNA strands
et17(1:pos(17))=T(i)+(et17(1:pos(17))-T(i))./tau_encap_old.*tau_encap; % encapsidation completion times for the (+)RNA strands
tau_encap_old=tau_encap; % set the old encapsidation time to the new one
% When the mean of the poisson distribution is big, N will be drawn from a normal distribution
if alpha(i)>=20
%% avoid some nuisance generation of complex values;
%% jbr, 12/21/2008
D = real(alpha(i));
D = max(0, D);
x(i,13) = round(alpha(i) + sqrt(D) * randn);
else
% Draw N from Poisson distribution
r3 = rand;
for j=1:length(facts)
%% avoid some nuisance generation of complex values;
%% jbr, 12/21/2008
D = real(alpha(i));
D = max(0, D);
p(j)=exp(-alpha(i))*1/facts(j)*D^(j-1); % Probability of N being 0,1,2,....
r3=r3-p(j);
if r3<0
x(i,13)=j-1;
break;
end;
end
end
% Stop simulation when tend (4 hours) is reached
if T(i)>tend
break
end
% Calculation of all reaction rates:
a(1) = 50*k1(1)*x(i,6)*x(i,18);
a(2) = k3*x(i,13)*x(i,1);
a(3) = 0;
a(4) = k1(1)*x(i,3)*x(i,18);
a(5) = k3*x(i,13)*x(i,4);
a(6) = 0;
a(7:12) = k1(1:6).*genomes(i).*x(i,18);
% If level of N is greater than the checksize (100), N will be created by a continuous Langevin reaction and not be drawn from the Poisson distribution
if x(i,13) there are continuous reactions
if flag_mult==0 % if there are continuous reactions
% Calculate the maximum step size:
% all continuous reaction rates
r_con=zeros(19,1); % r_con is used to calculate the next maximum continuous step (set to 1% change in the continuous states)
% this has to be done before the Langevin calculations, because we need the step size for the Langevin reaction rate calculations
% rd will later be used for the Langevin reaction rate calculation (only when the reactions are continous)
for j=13:19
rd(j)=a(j)*(1-flag(j));
end
r_con(13)=rd(13);
r_con(14)=rd(14);
r_con(15)=rd(15);
r_con(16)=rd(16);
r_con(17)=rd(17);
r_con(18)=rd(18);
r_con(19)=-rd(14)*274-rd(15)*279-rd(16)*557-rd(17)*240-rd(18)*2127; % Amino acid depletion (host resource)
% all current states to calculate the relative rate of change (I take the max of (100,w) because we don't want to divide through 0)
rr = r_con(13:19); % contiunous reaction rates
r_index = find(rr); % which reactions are continuous
r_new = rr(r_index); % r_new reacion rates are all non-zero
% last molecule level of continuous states:
w = x(i,13:19)';
w_new=w(r_index);
% time to change 100% in one state:
t_norm=w_new./r_new;
% maximum step: minimum of max_step and tolerance percentage multiplied with the smallest time
maxstep=min([max_step;tol*min(abs(t_norm))]);
end; %End of calculating the maximum step size.
check_step = 0;
% All stochastic reaction rates:
r=a.*flag;
% Sum of it:
a0 =sum(r);
if (a0 == 0) %If there are no stochastic reactions
step = maxstep;
check_step = 1;
else
%Find timestep:
step = (1/a0)*log(1/r1);
%Find reaction:
m=sum(cumsum(r)<=r2*a0)+1; %Calculating which reaction occurs
if step > maxstep
check_step = 1;
%If the step is too big, only let it go a little bit.
%This is fine because the timesteps are exponentially distributed (and so memoryless).
step = maxstep;
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%END OF STOCHASTIC CALCULATION%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Save current time for check of delayed reactions:
current_time=T(i)+step;
event_times=[et1(1) et2(1) et3(1) et4(1) et5(1) et6(1) et7(1) et8(1) et9(1) et10(1) et11(1) et12(1) et13(1) et14(1) et15(1) et16(1) et17(1)]; % All first event times
et=min(event_times); % first event time of all first event times
n=find(event_times==et); % which event comes first
n=n(1);
if et>current_time % if stored events are later than the next reaction:
%New states:
if m==0 % If no stochastic reaction (time step too big for continuous update) do nothing
else
z=v1(m,:); % else take the m-th row of the stoichiometric matrix v
end
% If reactions are delayed, store the completion of the reaction in seperate event vectors and move the pointer of the next free
% storage postition (makes storing and accesing the next event faster)
% m==7...12: transcription reactions
% m==1 and m==4: replication reactions
% m==2 and m==5: encapsidation reactions
if m==7
et1(pos(1))=current_time+tau(1);
et9(pos(9))=current_time+tau(1);
pos(1)=pos(1)+1;
pos(9)=pos(9)+1;
end;
if m==8
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et10(pos(10))=current_time+tau(2);
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(10)=pos(10)+1;
end;
if m==9
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et11(pos(11))=current_time+tau(3);
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(11)=pos(11)+1;
end;
if m==10
et4(pos(4))=current_time+tau(4);
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et12(pos(12))=current_time+tau(4);
pos(4)=pos(4)+1;
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(12)=pos(12)+1;
end;
if m==11
et5(pos(5))=current_time+tau(5);
et4(pos(4))=current_time+tau(4);
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et13(pos(13))=current_time+tau(5);
pos(5)=pos(5)+1;
pos(4)=pos(4)+1;
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(13)=pos(13)+1;
end;
if m==12
et6(pos(6))=current_time+tau(6);
et5(pos(5))=current_time+tau(5);
et4(pos(4))=current_time+tau(4);
et3(pos(3))=current_time+tau(3);
et2(pos(2))=current_time+tau(2);
et1(pos(1))=current_time+tau(1);
et14(pos(14))=current_time+tau(6);
pos(6)=pos(6)+1;
pos(5)=pos(5)+1;
pos(4)=pos(4)+1;
pos(3)=pos(3)+1;
pos(2)=pos(2)+1;
pos(1)=pos(1)+1;
pos(14)=pos(14)+1;
end;
if m==1
et7(pos(7))=current_time+tau(7);
et15(pos(15))=current_time+tau(7);
pos(7)=pos(7)+1;
pos(15)=pos(15)+1;
end;
if m==4
et8(pos(8))=current_time+tau(7);
et15(pos(15))=current_time+tau(7);
pos(8)=pos(8)+1;
pos(15)=pos(15)+1;
end;
if m==2
et16(pos(16))=current_time+tau_encap;
pos(16)=pos(16)+1;
end;
if m==5
et17(pos(17))=current_time+tau_encap;
pos(17)=pos(17)+1;
end;
else %if there are stored events that are earlier than the next reaction
step = et - T(i); % update to the next event time
z = v2(n,:); % add delayed reaction
% delete the first event of the event vector and move the pointer of the last event one spot to the left
switch n
case{1}
et1 = [et1(2:length(et1));inf];
pos(1)=pos(1)-1;
case{2}
et2 = [et2(2:length(et2));inf];
pos(2)=pos(2)-1;
case{3}
et3 = [et3(2:length(et3));inf];
pos(3)=pos(3)-1;
case{4}
et4 = [et4(2:length(et4));inf];
pos(4)=pos(4)-1;
case{5}
et5 = [et5(2:length(et5));inf];
pos(5)=pos(5)-1;
case{6}
et6 = [et6(2:length(et6));inf];
pos(6)=pos(6)-1;
case{7}
et7 = [et7(2:length(et7));inf];
pos(7)=pos(7)-1;
case{8}
et8 = [et8(2:length(et8));inf];
pos(8)=pos(8)-1;
case{9}
et9 = [et9(2:length(et9));inf];
pos(9)=pos(9)-1;
case{10}
et10 = [et10(2:length(et10));inf];
pos(10)=pos(10)-1;
case{11}
et11 = [et11(2:length(et11));inf];
pos(11)=pos(11)-1;
case{12}
et12 = [et12(2:length(et12));inf];
pos(12)=pos(12)-1;
case{13}
et13 = [et13(2:length(et13));inf];
pos(13)=pos(13)-1;
case{14}
et14 = [et14(2:length(et14));inf];
pos(14)=pos(14)-1;
case{15}
et15 = [et15(2:length(et15));inf];
pos(15)=pos(15)-1;
case{16}
et16 = [et16(2:length(et16));inf];
pos(16)=pos(16)-1;
case{17}
et17 = [et17(2:length(et17));inf];
pos(17)=pos(17)-1;
end;
end;
% Continuous Langevin reaction rate calculations
if flag_mult==0 % If there are continous reactions
rn = randn([5,1]); % normally distributed random number
for j=14:18
%% avoid some nuisance generation of complex values;
%% jbr, 12/21/2008
D = real(rd(j)*step);
D = max(0, D);
sd(j)=rd(j)*step+sqrt(D)*rn(j-13); % First order Langevin reaction rate
end
s_con(14)=sd(14);
s_con(15)=sd(15);
s_con(16)=sd(16);
s_con(17)=sd(17);
s_con(18)=sd(18);
s_con(19)=-sd(14)*274-sd(15)*279-sd(16)*557-sd(17)*240-sd(18)*2127;
r_con=s_con;
else
r_con=zeros(19,1);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%delta x (stochastic and Langevin part together)
z=z+r_con';
%update species
x(i+1,:) = x(i,:) + z;
%update time
T(i+1) = T(i) + step;
% if (mod(i,5000)==0)
% fprintf(1,'i=%3d T=%3.2f ',i,T(i));
% end;
end %main loop
message = ['End of run ',num2str(u),' with ',num2str(i),' iterations']
index_old=1;
index=zeros(tfinal+1,1);
for j=1:length(time_vec)
index(j)=searcht(index_old,T,time_vec(j),i,0)-1;
index_old=index(j);
end
% Save all states of all runs in new vectors
for c=1:18
eval(['x',num2str(c),'(:,u)=x(index,c);'])
end
end
save xmean.debug
g1 = x1+x2+x3; % all (-)RNA genomes
g2 = x4+x5+x6; % all (+)RNA genomes
x_mean1 = [mean(g1,2), mean(g2,2)]; % mean of genomes
x_mean2 = [mean(x7,2), mean(x8,2), mean(x9,2), mean(x10,2), mean(x11,2), mean(x12,2)]; % mean of mRNAs
x_mean3 = [mean(x13,2), mean(x14,2), mean(x15,2) mean(x16,2), mean(x17,2), mean(x18,2)]; % mean of proteins
f1=0:1400:140000; % bins for the GFP distribution
GFP35=x17(12601,:); % GFP level at 3.5 hours
GFP4=x17(14401,:); % GFP level at 4 hours
[zz,yy]=hist(GFP35,f1); % create history of GFP level at 3.5 hours
table4=[yy' zz']; % distibution table of GFP at 3.5 hours
[zz,yy]=hist(GFP4,f1); % create history of GFP level at 4 hours
table5=[yy' zz']; % distibution table of GFP at 4 hours
f2=0:30:3000; % bins for the RNA distribution
RNA25=g1(9001,:); % (-)RNA level at 2.5 hours
RNA3=g1(10801,:); % (-)RNA level at 3 hours
RNA4=g1(14401,:); % (-)RNA level at 4 hours
[zz,yy]=hist(RNA25,f2); % create history of RNA level at 2.5 hours
table6=[yy' zz']; % distibution table of RNA at 2.5 hours
[zz,yy]=hist(RNA3,f2); % create history of RNA level at 3 hours
table7=[yy' zz']; % distibution table of RNA at 3 hours
[zz,yy]=hist(RNA4,f2); % create history of RNA level at 4 hours
table8=[yy' zz']; % distibution table of RNA at 4 hours
table1 = [time_vec/3600, x_mean1];
table2 = [time_vec/3600, x_mean2];
table3 = [time_vec/3600, x_mean3];
table9 = [x12(5400,:)' g1(14401,:)']; % create table for LmRNA, (-)RNA dependency
save genomes.dat table1
save mRNAs.dat table2
save proteins.dat table3
save GFPdist35.dat table4
save GFPdist4.dat table5
save RNAdist25.dat table6
save RNAdist3.dat table7
save RNAdist4.dat table8
save LmRNA.dat table9
Main Script
